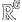This letter explores the continuity characteristics of value functions associated with optimal control in circadian rhythm entrainment problems. Our results demonstrate that when the optimal objective is to minimize the time required for entrainment, the corresponding value function is not Lipschitz continuous. This lack of Lipschitzianity suggests that the optimal cost and optimal trajectory are not robust under perturbation. As an alternative, we propose a new objective function that is based on the cumulative squared tracking error and show that the resulting value function is Lipschitz continuous. Through numerical simulations, we further establish that data-driven feedback control systems exhibit higher robustness to input perturbation when the data are collected from optimal control solutions that minimize the cumulative squared tracking error, as opposed to those that are time-optimal.
IEEE Control Systems Letters, Vol 8, May 28 2024, pp. 952-975.